菊芋微波真空干燥过程的水分扩散特性及模型拟合

程新峰; 潘玲; 李宁; 陈佳强

doi:10.13386/j.issn1002-0306.2021070048

菊芋微波真空干燥过程的水分扩散特性及模型拟合

程新峰^1,,
潘玲¹,
李宁^2, ,,
陈佳强²

1.
安徽师范大学生态与环境学院，安徽芜湖 241000
2.
安徽师范大学生命科学学院，安徽芜湖 241000

基金项目: 安徽省自然科学基金项目（2008085MC103）；安徽高校自然科学研究重点项目（KJ2019A0495）；江南大学食品科学与技术国家重点实验室开放课题（SKLF-KF-201903）；国家级大学生创新创业训练计划项目（202010370227）。

详细信息

作者简介:
程新峰（1981−），男，博士，副教授，研究方向：农业资源综合利用与开发，E-mail：chxf0110194@163.com

通讯作者:
李宁（1989−），女，硕士，讲师，研究方向：果蔬精深加工及副产品综合利用，E-mail：shning1989@ahnu.edu.cn

中图分类号: TS255.1
计量
- 文章访问数: 214
- HTML全文浏览量: 72
- PDF下载量: 16
出版历程
- 收稿日期: 2021-07-04
- 录用日期: 2022-01-05
- 网络出版日期: 2022-01-14
- 刊出日期: 2022-03-14

Moisture Diffusivity Characteristics and Model Fitting of Jerusalem Artichoke(Helianthus tuberosus L.) during Microwave Vacuum Drying

1.
School of Ecology and Environment, Anhui Normal University, Wuhu 241000, China
2.
College of Life Sciences, Anhui Normal University, Wuhu 241000, China

摘要

摘要: 为了探究菊芋微波真空干燥过程中水分变化规律，本文考察了不同微波强度对菊芋干燥特性的影响。采用Weibull分布函数和Dincer模型对干燥曲线进行拟合，并结合尺度参数(α)、形状参数(β)、滞后因子(G)、干燥系数(S)等分析了干燥过程的传热、传质机制。结果表明：除1.28 W/g外，菊芋整个干燥过程分为升速、恒速和降速3个阶段，且微波强度越大，最大干燥速率愈高，升速阶段历时越短。β介于1.314～2.175之间，表明干燥过程并非完全由内部扩散主导。G为1.043～1.188，且随微波强度增大而减小。毕渥数(Bi)介于0.179～5.762之间，说明干燥过程物料温度变化由内部导热和边界对流换热共同控制。基于Weibull分布函数、Dincer模型和Fick第二定律得到的水分扩散系数分别为D_cal=5.922×10⁻⁸～2.717×10⁻⁷ m²/s、D_eff=7.570×10⁻⁷～1.799×10⁻⁵ m²/s、D^*_eff=2.353×10⁻⁹～7.546×10⁻⁹ m²/s；同样微波强度下，其大小依次为：D_eff>D_cal>D^*_eff。2.32 W/g下，干燥样品亮度(L^*值)最大，为69.05。微波强度愈大，样品色泽参数a^*和b^*值越小。SEM图片显示：适宜的微波强度下，干燥菊芋细胞结构规则，部分区域含有孔洞；1.28 W/g样品的细胞皱缩明显，而高微波强度下(2.70和3.04 W/g)干燥样品部分组织结构坍塌，细胞内物质外泄。
- 微波真空干燥 /
- Weibull分布函数 /
- Dincer模型 /
- 水分扩散系数 /
- 活化能
Abstract: To explore the law of moisture variation in Jerusalem artichoke during microwave vacuum drying process, the effects of microwave intensity on the drying characteristics of Jerusalem artichoke were investigated. The Weibull distribution function and Dincer model were used to fit the drying curves, and the heat and mass transfer mechanism during drying process were analyzed by using the model parameters, namely scale parameter (α), shape parameter (β), lag factor (G) and drying coefficient (S). The results showed that there were three stages of rising rate, constant rate and falling rate under all the microwave intensity levels, except for the intensity level of 1.28 W/g. The higher the microwave intensity, the larger the maximum drying rate, and the shorter the duration of rising rate stage. The shape parameter (β) ranged from 1.314 to 2.175, which indicated that the drying process of Jerusalem artichoke was not completely controlled by internal water diffusion. The lag factor (G) ranged from 1.043 to 1.188, and decreased with the microwave intensity increased. The values of Biot number (Bi) located in the range of 0.179 and 5.762, which indicated that the temperature changes of sample in the drying process were controlled by internal thermal conductivity and boundary convective heat transfer. Effective moisture diffusion coefficients calculated by Weibull distribution function, Diner model and Fick’s second law were (D_cal=5.922×10⁻⁸~2.717×10⁻⁷ m²/s), (D_eff =7.570×10⁻⁷~1.799×10⁻⁵ m²/s), and (D^*_eff=2.353×10⁻⁹~7.546×10⁻⁹ m²/s), respectively. Under the same microwave intensity, their values were in order: D_eff>D_cal >D^*_eff. The maximum value of brightness (L^*) for dried samples was 69.05 under the microwave intensity level of 2.32 W/g. Both color parameters a^* and b^* decreased with the increasing of microwave intensities. SEM figures showed that the cell structure in dried Jerusalem artichoke was regular, and exhibited obvious pore characteristics when applying suitable microwave intensity. The tissue structure of dried samples shrank obviously at microwave intensity of 1.28 W/g, while part of the tissue structure collapsed and the intracellular material condensed at higher microwave intensities of 2.70 and 3.04 W/g.
- microwave vacuum drying /
- Weibull distribution function /
- Dincer model /
- moisture diffusion coefficient /
- activation energy

HTML全文

菊芋（Helianthus tuberosus L.），又称洋姜、鬼子姜，是菊科向日葵属的一种多年生草本植物。菊芋最早产于北美洲，17世纪由欧洲传入中国，现今已在中国及广大东南亚地区广泛种植^[1]。菊芋块茎具有较好的营养及药用价值，不仅含有丰富的维生素、矿物质、菊芋多糖等成分^[2]，还具有清热解毒、抗菌消炎、降低血糖等功效^[3]。新鲜菊芋水分含量高，不易贮藏，干制是其常见保藏方式之一。Tamás等^[4]报道，相比冷冻干燥，菊芋采用中红外-冷冻联合干燥缩短了15%～40%的干燥时间，同时改善了色泽，提高了产品的硬度。Doymaz等^[5]在60～80 ℃对菊芋进行了热风干燥，发现在实验温度范围内菊芋的水分扩散系数为5.49×10^–10～1.90×10⁻⁹ m²/s，且随温度升高而增大。然而，有关菊芋块茎微波真空干燥及过程控制的研究还鲜有报道，有待于进一步探索。

微波真空干燥是在真空条件下采取微波加热而脱去物料水分的加工方式，由于同时兼备微波瞬时加热和真空干燥低温的特点^[6-7]，目前该技术已被用于双孢菇^[8]、榴莲^[9]、猕猴桃^[6]、香蕉^[10]、甘薯^[11]、罗非鱼片^[12]等农副产品的加工。脱水产品品质、能耗与物料内水分扩散机制密切相关，但现有技术还难以在线监测物料干燥过程的水分变化情况。因此，国内外学者提出了一些理论、经验及半经验模型，如Lewis、Page、Two-Terms等用于描述干燥过程物料内部水分的变化规律^[13-14]，但这些模型涉及的参数缺乏物理意义，无法揭示干燥期间传热、传质规律，对干燥条件选择也无指导作用。与上述模型不同，Weibull分布函数的尺度参数（α）和形状参数（β）与干燥过程热、质传递有关，可用于求解估算水分扩散系数和判定干燥过程是否有升速阶段^[6,12]；而Dincer模型的滞后因子（G）和干燥系数（S）则能用于评价干燥过程中规则物料（如平板型、圆柱状、球状）的传热、传质规律^[15-16]。基于Weibull和Dincer模型学者已成功分析了光皮木瓜^[16]和枸杞^[17]真空脉冲干燥过程物料内传热、传质规律。然而，关于菊芋微波真空干燥过程中热、质传递规律方面的研究还未见报道。

因此，本文以菊芋为对象，基于Weibull分布函数和Dincer模型对物料微波真空干燥过程的水分扩散特性，传热、传质机制进行了分析，并通过模型参数计算干燥过程物料内有效水分扩散系数和活化能。同时，还对干燥产品的色泽和微观结构进行分析，以期为菊芋微波真空过程控制及品质监控提供指导。

1. 材料与方法

1.1 材料与仪器

新鲜菊芋（Helianthus tuberosus L.）　徐州盛通食品有限公司，选取大小一致，色泽均一、无损伤的菊芋块茎置于4±1 ℃冰箱中待用。

ORW1.0S-5Z型微波真空干燥设备　南京奥润微波科技有限公司；DHG-9101-3S型电热恒温鼓风干燥箱　金坛市杰瑞尔电器有限公司；Quanta FEG450型扫描电子显微镜　美国FEI公司；FA1004型电子天平　常州幸运电子科技有限公司；CR-400型色差仪　日本柯尼卡美能达株式会社。

1.2 样品制备与处理

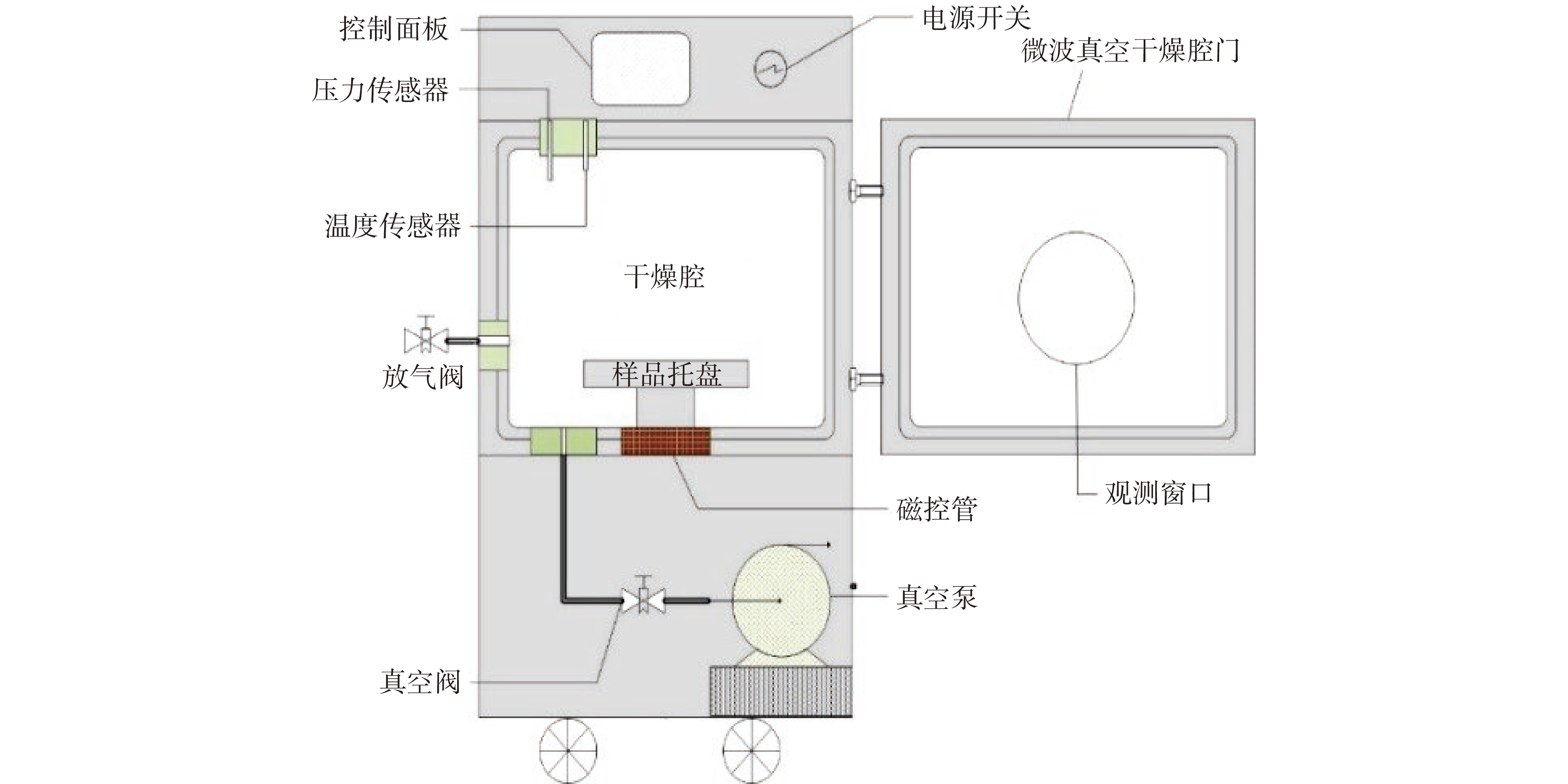
将菊芋块茎洗净后，去皮，然后切成厚度4 mm，直径2.5 cm的圆柱状。称取100 g左右样品平铺于物料托盘上，然后放入微波真空干燥设备（如图1所示）脱水干燥。干燥过程中每隔1.5 min取出样品称量并记录数据，直至样品干基含水量低于0.10 g/g为止。

图 1 微波真空干燥设备示意图

Figure 1. Schematic diagram of microwave vacuum drying equipment

下载: 全尺寸图片幻灯片

设备参数：真空度−90 kPa，微波功率分别为200、400、600、800和1000 W。依据文献[8]测定不同额定功率下的设备实际输出功率（P），然后算出它们对应微波强度分别1.28、1.69、2.32、2.70和3.04 W/g。

1.3 干燥曲线拟合及参数计算方法

1.3.1 干燥参数计算

依据GB 5009.3-2016的方法，将菊芋放入105 ℃恒温干燥箱内，至试样质量不再变化为止，其中新鲜菊芋的干基水分含量为4.186±0.364 g/g。水分比（MR）表示干燥过程物料水分含量的变化，计算公式可简化为^[12]：

$\rm MR = \frac{{{M_t}}}{{{M_0}}}$

(1)

式中，M_t为物料在t时刻的干基含水率，g/g；M₀为物料初始干基含水率，g/g。

干燥速率（DR）计算公式为^[12]：

$\rm DR = \frac{{{M_{t + \Delta t}} - {M_t}}}{{\Delta t}}$

(2)

式中：DR为时刻t至t+Δt时间段的干燥速率，g/（g min）；M_t和M_t+Δt分别为时刻t与t+Δt的干基含水率，g/g；Δt为相邻两次测量的时间差，min。

1.3.2 Weibull分布函数

Weibull分布函数的表达式如式（3）所示：

$\rm MR = \exp \left[ { - {{\left( {\frac{t}{\alpha }} \right)}^\beta }} \right]$

(3)

式中：α为尺度参数，其值约为物料脱去63%水分所需的时间，min；β为形状参数，与干燥起始速率及物料内水分迁移机制有关^[18]；t为干燥时间，min。Weibull分布函数可用于干燥过程水分扩散系数（D_cal）的估算，计算公式如下^[12]：

$\rm {D_{cal}} = \frac{{{r^2}}}{\alpha }$

(4)

式中：D_cal为估算的水分扩散系数，m²/s；r为物料的体积等效半径，即菊芋片等体积的球的半径，为7.768×10⁻³ m。

1.3.3 Dincer模型

Dincer模型，又称Bi-G模型，如式（5）所示^[19-20]：

$\rm MR = G\exp ( - St)$

(5)

式中：G为滞后因子，用于表征干燥过程中热、质传递受到内部阻力的大小；S为干燥系数，表示单位时间内干燥能力的大小，S值越大，则干燥速率越快；t为干燥时间，min。毕渥数（Bi）和水分有效扩散系数（D_eff）分别由公式（6）和（7）计算获得。

$\rm Bi = 0.0576{G^{26.7}}$

(6)

$\rm {D_{eff}} = \frac{{S{L^2}}}{{{\mu ^2}}}$

(7)

式中：L为物料厚度，0.004 m；μ为特征式（8）的根^[15]。

$\rm \mu = - 3.4775{G^4} + 25.285{G^3} - 68.43{G^2} + 82.468G - 35.638$

(8)

结合式（6）和（7）得出对流传质系数（k）^[21]。

$\rm k = \frac{{2{D_{eff}}Bi}}{L}$

(9)

1.3.4 水分有效扩散系数（D^*_eff）计算

降速干燥阶段物料内水分迁移规律可以用简化的Fick第二定律来描述，其表达式为^[12,19]：

$\rm MR = \frac{8}{{{\text{π} ^2}}}\exp \left( { - \frac{{{\text{π} ^2}D_{eff}^*}}{{{L^2}}}t} \right)$

(10)

式中：D^*_eff为有效水分扩散系数，m²/s；L为物料厚度，为0.004 m；t为干燥时间，s。将式（10）转化成线性形式，然后依据直线的斜率就能计算出有效水分扩散系数。

1.3.5 活化能计算

据文献[6,22]报道，干燥过程中物料的有效水分扩散系数D^*_eff与微波强度的关系符合阿伦尼乌斯（Arrhenius）方程，计算公式为：

$\rm D_{eff}^* = {D_o}\exp \left( {{{ - }}\frac{{{E_a}m}}{P}} \right) = {D_o}{\text{exp}}\left( {{{ - }}\frac{{{E_a}}}{I}} \right)$

(11)

式中，E_a为活化能，kJ/mol；m为装载量，g；P为微波实际输出功率，W；I为微波强度，W/g；D₀ 为Arrhenius方程指数前因子，m²/s。将式（11）两边取对数，然后对ln （D^*_eff） vs I进行线性拟合，即可得到活化能E_a。

1.4 色泽测定

采用CR-400色差仪测量样品的L^*、a^*和b^*值，每组样品10个重复。参阅文献[23-24]，采用色差值（ΔE）对样品进行综合评价，计算公式如下：

$\Delta E = \sqrt {{{\left( {{L^ \text{*} } - {L_0}} \right)}^2} + {{\left( {{a^ \text{*} } - {a_0}} \right)}^2} + {{\left( {{b^ \text{*} } - {b_0}} \right)}^2}}$

(12)

式中： ${L^ \text{*} }$ 值为干制品亮度指数； ${a^ \text{*} }$ 值为红-绿指数； ${b^ \text{*} }$ 值为蓝-黄指数；L₀、a₀和b₀为新鲜样品对应的色泽参数。

1.5 微观结构观察

将干燥样品固定在碳导电胶上，抽真空喷金处理3 min，然后用FEI Quanta 450电子显微镜在30 kV加速电压下对样品表面组织微观结构进行观察。在不同的放大倍数下，重复观察样品，并保存代表性区域的图片以供进一步分析。

1.6 数据处理

采用Origin8.5软件对实验数据进行回归分析，并以决定系数（R²）及均方根误差（RMSE）评价拟合效果好坏，其中R²越大，RMSE越小，模型的拟合效果越好。R²和RMSE的计算公式如下：

${R^2} = \rm 1 - \frac{{\displaystyle\sum\nolimits_{i = 1}^N {{{\left( {M{R_{pre,i}} - M{R_{\exp ,i}}} \right)}^2}} }}{{\displaystyle\sum\nolimits_{i = 1}^N {{{\left( {\overline {MR}_{{{pre,i}}} - M{R_{{\text{exp}},{\text{i}}}}} \right)}^2}} }}$

(13)

$\rm RMSE = {\left( {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{\left( {M{R_{pre,i}} - M{R_{exp,i}}} \right)}^2}} } \right)^{1/2}}$

(14)

式中：MR_{exp, i}为实验测得的第i个水分比；MR_{pre, i}为模型预测的第i个水分比； $\rm {\overline {MR} _{\exp ,i}}$ 为实验所得水分比的平均值；N为实验测定数据的个数。

实验结果以 $\overline {\rm{x}} \pm {\rm{SD}}$ 表示。采用SPSS18.0软件进行单因素方差分析（one-way ANOVA），数据间差异显著性检验用Duncan法，显著性水平设定在α=0.05。

2. 结果与分析

2.1 菊芋微波真空干燥特性

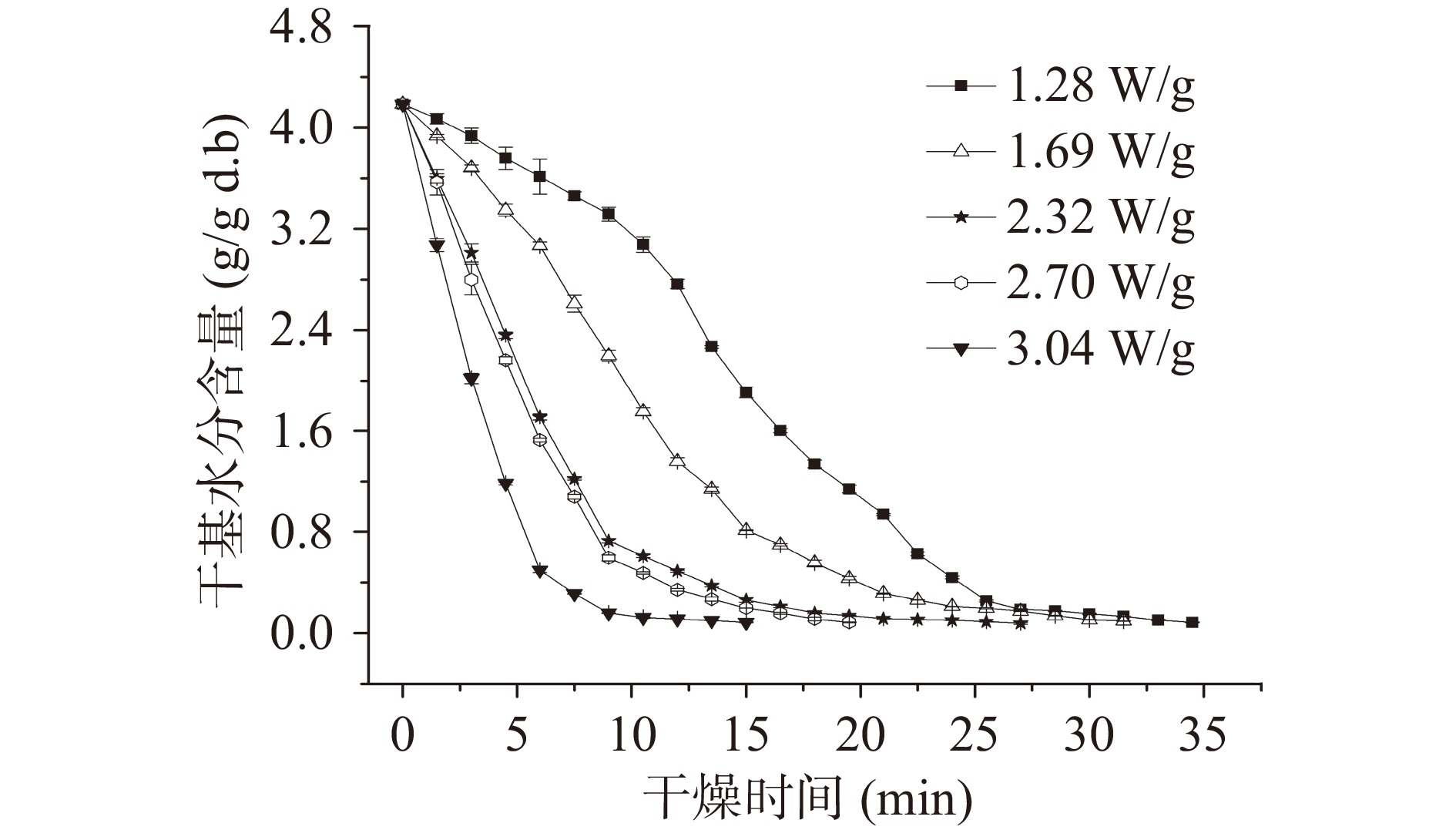
图2是物料厚度为4 mm，真空度为−90 kPa时菊芋的微波真空干燥曲线。由图2可见，随着干燥的进行，物料水分逐渐减少。其中微波强度为1.28、1.69、2.32、2.70和3.04 W/g时，物料干基含水率降至0.10 g/g （d.b）以下所需的时间分别为34.5、31.5、25.5、19.5和15 min，说明微波强度越大，物料脱水速率越快，所需干燥时间越短，这与微波真空干燥香蕉^[10]和猕猴桃^[25]所得结果一致。与1.28 W/g相比，3.04 W/g下物料干燥时间缩短了56.52%，这是因为微波强度越大，单位时间内设备释放的微波能越多，物料内极性水分子汽化的速率越快，因而大大缩短了干燥时间，提高了干燥效率。

图 2 不同微波强度下菊芋片的干燥曲线

Figure 2. Drying curves of jerusalem artichoke slices under different levels of microwave intensity

下载: 全尺寸图片幻灯片

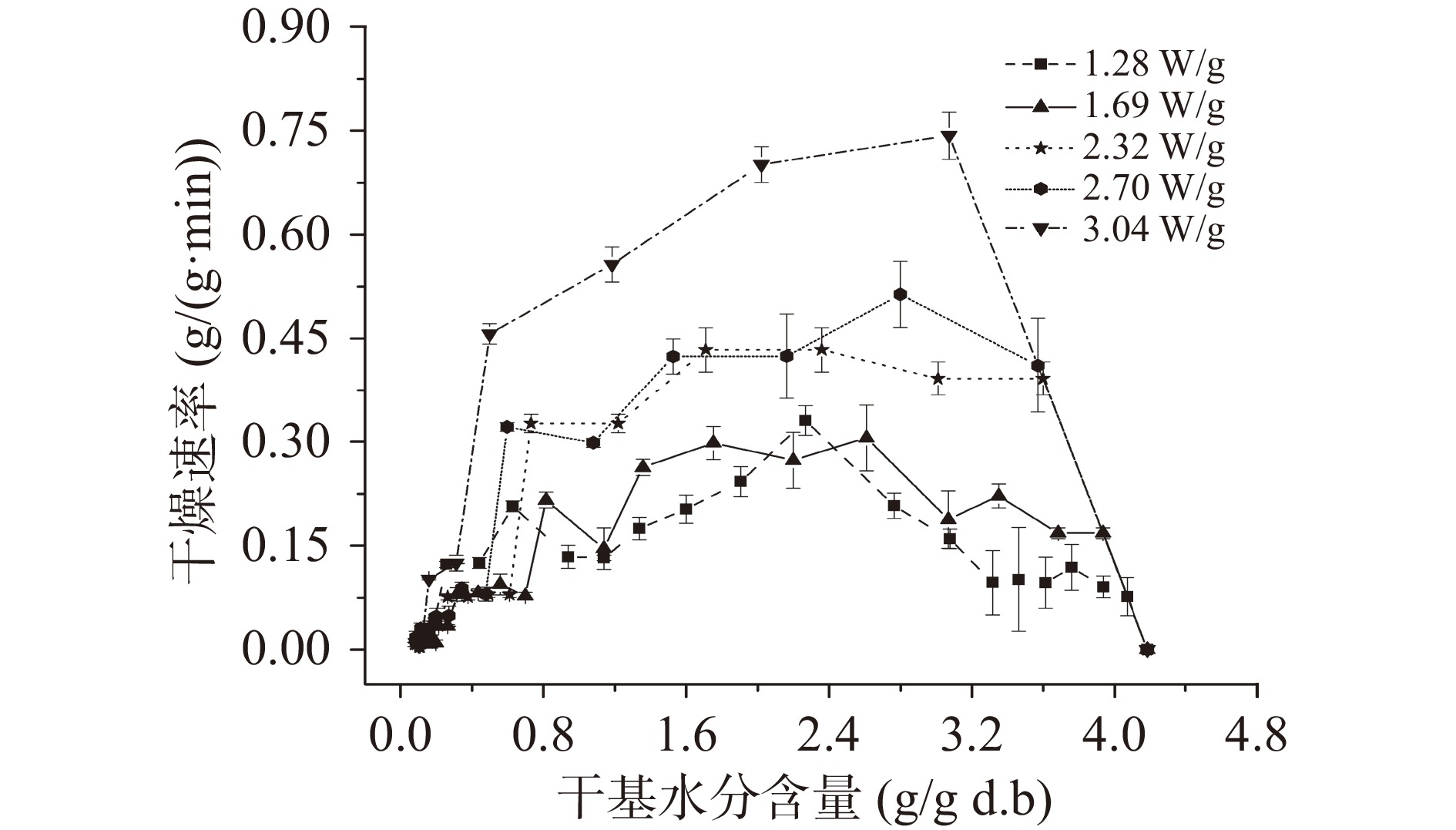
由图3可知，物料干燥速率变化较大，且随着微波强度的增大变化的幅度越大。微波强度为1.28 W/g时，干燥前期物料有一个缓慢的升速阶段，至13.5 min时干燥速率达到最大值（0.3306 g/（g·min）），之后干燥速率逐渐下降，即为降速干燥阶段。其它微波强度下，整个干燥过程均存在升速、恒速和降速3个干燥阶段，但不同微波强度下，物料升速干燥阶段所需时间和干燥速率最大值不同。微波强度越大，物料升速干燥所需时间越短，且最大干燥速率越高，如3.04 W/g下最大干燥速率为0.743 g/（g·min），是1.69 W/g下0.306 g/（g·min）的2倍多。干燥前期存在升速阶段，一方面，由于物料含有较高的水分含量，能吸收微波能产生摩擦热，致使物料内部与表面形成温度梯度；另一方面，物料表面水分汽化形成的水蒸气可被真空泵迅速抽走，故物料内外也存在较大的湿度梯度。同时，微波强度越大，单位时间内物料吸收微波能越多，产生大量的摩擦热，致使干燥速率增大。随着干燥进行，物料水分含量逐渐减少，微波能吸收能力下降，且干燥导致的内部结构变化也会妨碍水分迁移，因此干燥后期表现为降速干燥阶段^[25]。刘春泉等^[26]在杏鲍菇微波真空干燥研究中，也发现物料干燥过程分为升速、恒速和降速3个阶段，且功率越大，升速阶段失水速率曲线越陡，历时越短。

图 3 不同微波强度下菊芋片的干燥速率曲线

Figure 3. Curves of drying rates of Jerusalem artichoke slices at different levels of microwave intensity

下载: 全尺寸图片幻灯片

2.2 微波真空干燥曲线拟合结果分析

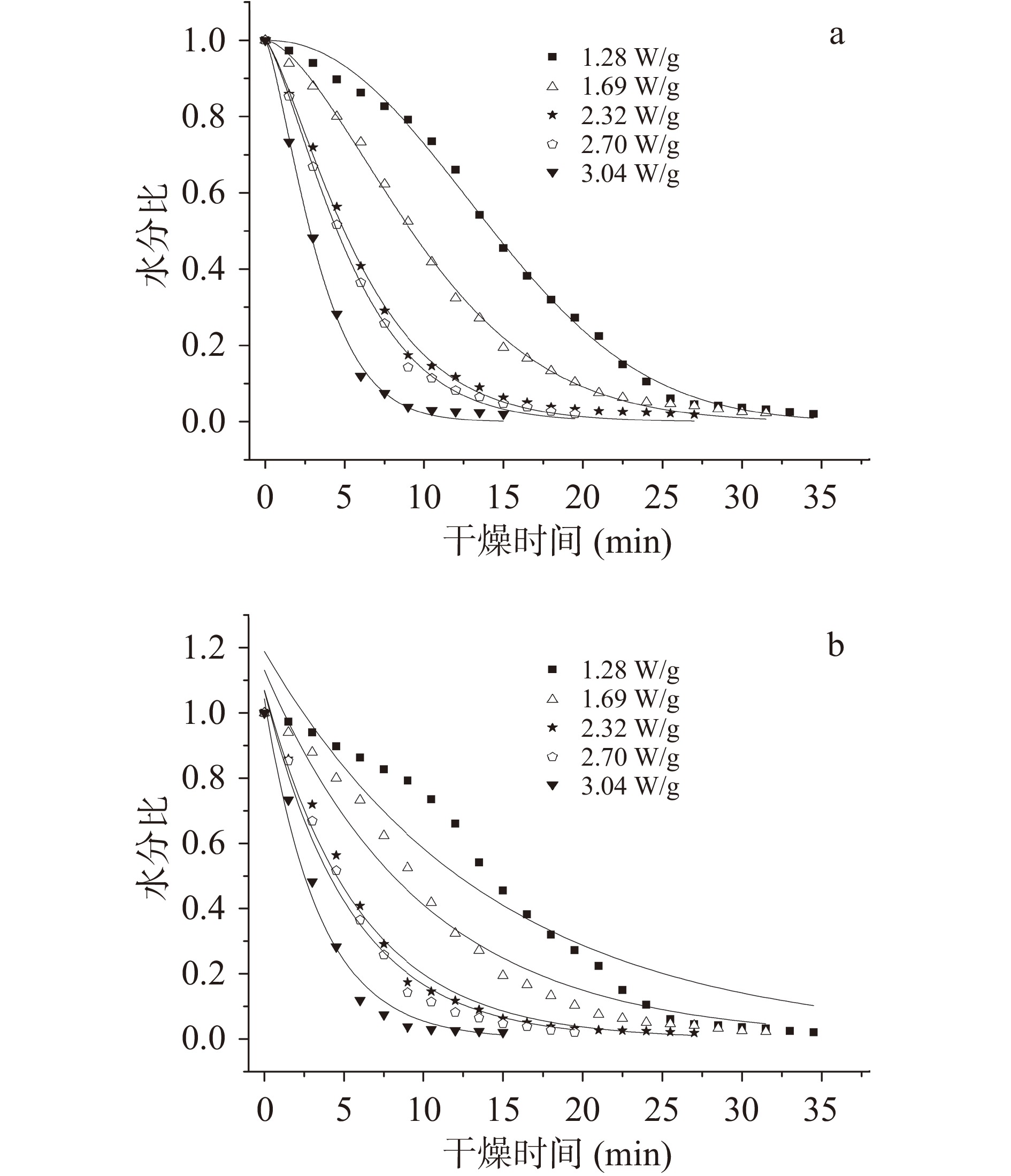
基于最小二乘法，采用Weibull分布函数对菊芋片微波真空干燥曲线进行拟合，结果如表1和图4a所示。由表1可知，决定系数（R²）在0.996～0.998之间，均方根误差（RMSE）在0.0134～0.0213之间，表明Weibull分布函数对菊芋片微波真空干燥过程拟合效果较好。尺度参数（α）与干燥速率有关，表示完成63%的干燥过程需要的时间^[6]。从表1中可以看出，微波强度从1.28 W/g增加到3.04 W/g，对应的α值也从16.983 min降低到3.701 min，减少了78.21%，可见微波强度增大可显著缩短干燥时间（P<0.05）。形状参数（β）与物料在干燥初始阶段的水分迁移机制相关，当β在0.3～1.0时，干燥速率由内部水分扩散控制为主，表现为降速干燥的特点；当β>1时，表明干燥前期存在延滞阶段，干燥过程由内外部水分扩散共同控制^[27]。由表1可知，不同微波强度下物料干燥过程的β值在1.314～2.175之间，且微波强度越大，β值越小，表明菊芋干燥前期存在延滞现象，且整个过程并非完全由内部扩散控制，这与干燥速率曲线的变化趋势相一致。类似的结论在猕猴桃切片^[6]和罗非鱼片^[12]的微波真空干燥中也有报道。

表 1 基于Weibull分布函数和Dincer模型的菊芋干燥曲线拟合结果

Table 1. Simulation results of drying curves of Jerusalem artichoke slices based on Weibull and Dincer model

微波强度（W/g）	Weibull 分布模型				Dincer模型
微波强度（W/g）	尺度参数α （min）	形状参数β	R²	RMSE	滞后因子G	干燥系数S （s^-1）	R²	RMSE
1.28	16.983±0.16^a	2.175±0.06^a	0.996	0.0213	1.188±0.07^a	0.071±0.006^a	0.910	0.105
1.69	11.581±0.11^b	1.598±0.03^b	0.998	0.0150	1.131±0.04^ab	0.101±0.006^b	0.966	0.0601
2.32	6.563±0.11^c	1.314±0.04^c	0.996	0.0180	1.069±0.03^bc	0.168±0.007^c	0.986	0.0345
2.70	5.958±0.08d	1.330±0.03^c	0.998	0.0134	1.067±0.03^bc	0.185±0.010^c	0.985	0.0378
3.04	3.701±0.07^e	1.341±0.05^c	0.998	0.0150	1.043±0.03^c	0.293±0.018^d	0.985	0.0373
注：同列数据不同字母表示数据间存在显著性差异（P<0.05）；表2同。

下载: 导出CSV

| 显示表格

图 4 不同微波强度下Weibull分布函数（a）和Dincer模型（b）的预测值与试验值比较

Figure 4. Comparison of the predicted values by the Weibull (a) and Dincer (b) model and experimental values of moisture ratio at varying time under different microwave intensities

下载: 全尺寸图片幻灯片

Dincer模型拟合结果如表1和图4b所示，由R²（0.910～0.986）和RMSE（0.0345～0.105）可知，Dincer模型能较好地描述菊芋微波真空干燥过程水分比与干燥时间的关系。不同微波强度下的滞后因子（G）介于1.043～1.188之间，表明物料干燥前期具有升速阶段，且G值越大，升速阶段所需时间越长，这与Weibull分布函数中β值分析得到的结论一致。干燥系数（S）表示单位时间内物料的脱水能力，干燥速率越大，S值越大^[16]。本研究中，当微波强度为1.28 W/g时，G值最大，为1.188；S值最小，为0.071 s⁻¹。

基于Dincer模型参数G和S计算得到的传热毕渥数（Bi）和传质系数（k），如表2所示。Bi是物料内部导热热阻与表面对流换热热阻的比值^[20]，据文献[16,19]报道，当Bi值介于0～0.1之间时，物料温度变化取决于外界对流换热强度，可以忽略内部热阻的影响；当0.1<Bi<100则表示物料温度变化受内部导热热阻和表面对流换热热阻共同控制；当Bi>100说明物料温度变化完全由内部导热热阻控制。本文中Bi值介于0.179～5.762之间，且微波强度越高，Bi值越小，说明干燥过程菊芋温度变化由内部导热热阻和表面对流换热热阻共同决定。Ju等^[19]发现在热风干燥过程中不同厚度山药片传热机制存在差异，其中厚度为6 mm时，物料的温度变化由外界对流换热热阻决定；但厚度为12或18 mm时，物料温度变化由内部导热热阻和外界对流换热热阻共同控制。由公式（9）计算的传质系数（k）的大小介于1.035×10⁻³～2.181×10⁻³，明显高于光皮木瓜在气体射流冲击干燥过程中的传质系数（8.85×10⁻⁶～1.81×10⁻⁵）^[16]，这可能与微波快速加热及物料属性差异有关。

表 2 Weibull分布函数和Dincer模型参数的计算结果

Table 2. Results of Weibull and Dincer model parameters

微波强度（W/g）	D^*_eff （×10⁻⁹， m²/s）	D_cal （×10⁻⁸， m²/s）	D_eff （×10⁻⁷， m²/s）	毕渥数 Bi	特征根 μ	传质系数k （×10⁻³，m/s）
1.28	2.353±0.16^e	5.922±0.05^e	0.7570±0.04^a	5.762±0.29^a	1.225 ±0.06^a	2.181±0.11^a
1.69	2.872±0.10^d	8.684±0.08^d	1.646±0.08^b	1.543±0.08^b	0.991±0.05^b	1.270±0.06^c
2.32	4.138±0.09^c	15.326±0.25^c	5.954±0.30^c	0.348±0.02^c	0.672±0.03^c	1.035±0.05^d
2.70	4.982±0.14^b	16.881±0.22^b	6.844±0.34^d	0.328±0.02^c	0.658±0.03^c	1.122±0.06^d
3.04	7.546±0.32^a	27.178±0.51^a	17.985±0.90^e	0.179±0.009^c	0.511±0.03^d	1.610±0.08^b
注：“D^*_eff”表示依据Fick第二定律的计算得到的水分扩散系数；“D_cal”表示基于Weibull分布函数的计算结果；“D_eff”表示基于Dincer模型的计算结果。

下载: 导出CSV

| 显示表格

2.3 有效水分扩散系数及活化能的确定

水分扩散系数是一个描述物料内在水分扩散特性的动态量，其大小不仅与物料结构、组分、水分状态等因素相关，更取决于干燥方式和干燥条件，涉及分子扩散、吸水动力学流及毛细管流等^[12]。从表2中可以看出，基于Weibull分布函数α值估算的水分扩散系数（D_cal）在5.922×10⁻⁸～2.717×10⁻⁷ m²/s之间，而依据Fick第二定律得到的D^*_eff值介于2.353×10⁻⁹～7.546×10⁻⁹ m²/s之间，且两者均随微波强度增加而增大。比较发现，相同微波强度下D_cal均大于D^*_eff，因为D^*_eff计算的前提是整个干燥过程必须始终处于降速阶段，忽略干燥前期短暂升速阶段及后期物料收缩对水分迁移带来的影响，因此D^*_eff常被低估；而D_cal值则无需考虑干燥过程中物料水分扩散特点。基于Dincer模型求解得出的D_eff值在7.570×10⁻⁷～1.799×10⁻⁵ m²/s之间，且同一微波强度下，D_eff均高于D^*_eff和D_cal，因为D_eff计算综合考虑了物料内部导热热阻、外界对流换热热阻及传质系数的影响。张卫鹏等^[15]在茯苓中短波红外联合气体射流干燥研究中也得到了类似的结论，但在光皮木瓜干燥过程中，基于Dincer模型得到的D_eff值（3.26×10⁻⁹～6.33×10⁻⁸ m²/s）却低于Weibull模型计算的Dcal值（1.66×10⁻⁸～1.13×10⁻⁷ m²/s）^[16]。

活化能（E_a）是干燥过程中脱去1 mol水分需要的启动能量，其值大小与干燥的难易程度和能耗有关^[6]。基于公式（11）可得到菊芋微波真空干燥的E_a为2.306 kJ/（mol·K），这与微波真空干燥猕猴桃切片的活化能相差不大（−90 kPa下其大小为1.57108 kJ/mol）^[6]，但却与微波真空干燥双孢菇（高达18.05 kJ/mol）^[28]和龙眼果肉（180 Pa下高达9.021 kJ/mol）^[29]的活化能显著不同，这是因为物料分子结构、物质组成，预处理方式、干燥条件等存在差异。

2.4 色泽和微观结构分析

色泽是评价产品质量好坏的指标之一。如表3和图5所示，与新鲜样品相比，除1.28 W/g的干燥样品，其它干燥菊芋的L^*值显著增大（P<0.05），这与光的反射性能有关，因为干燥导致物料水分流失和结构变化均会对光的反射性能产生一定的影响，在干燥山药片^[20]和西洋参^[30]的研究中也有类似报道。随微波强度增大，干燥样品的L^*值呈先增加后下降的趋势，在2.32 W/g下，样品L^*值69.05，显著高于 1.28 W/g和1.69 W/g下样品的L^*值（P<0.05），但与2.70 W/g和3.04 W/g下的L^*值无显著差异（P>0.05）。干燥期间物料L^*值大小不仅与光的反射有关，同时与物料褐变程度相关。在较低的微波强度下，物料单位时间内吸收微波能少，干燥持续时间久，有利于美拉德反应和酶促褐变的发生。高微波强度下，物料干燥速率相对较快，能减轻美拉德反应引起褐变，但快速的汽化速率，可能会导致细胞内色素外泄，因而，样品的L^*值有所下降。由表3可知，干燥后样品的a^*和b^*值均显著增大（P<0.05），这是因为物料干燥期间发生了褐变，包括干燥前期短暂的酶促褐变和后期的美拉德反应^[31]。就不同微波强度而言，强度越大a^*、b^*值越小，如1.28 W/g下样品的a^*和b^*值分别为5.89和21.37，显著高于（P<0.05）其他处理组。如前所述，微波强度越大，干燥历时短，发生美拉德反应程度较低，同时，色素外露和降解也是a^*、b^*值下降的原因。ΔE是衡量样品色泽差异程度的指标，其值越大表明色泽变化越大。据报道^[23]，当ΔE>3时表明色泽差异非常明显，而ΔE<1.5则表示颜色差异较小。从表3可知，样品ΔE值均大于3，说明干燥使菊芋片色泽发生了明显的变化，尤其是1.28 W/g下的样品，其ΔE值高达10.67。

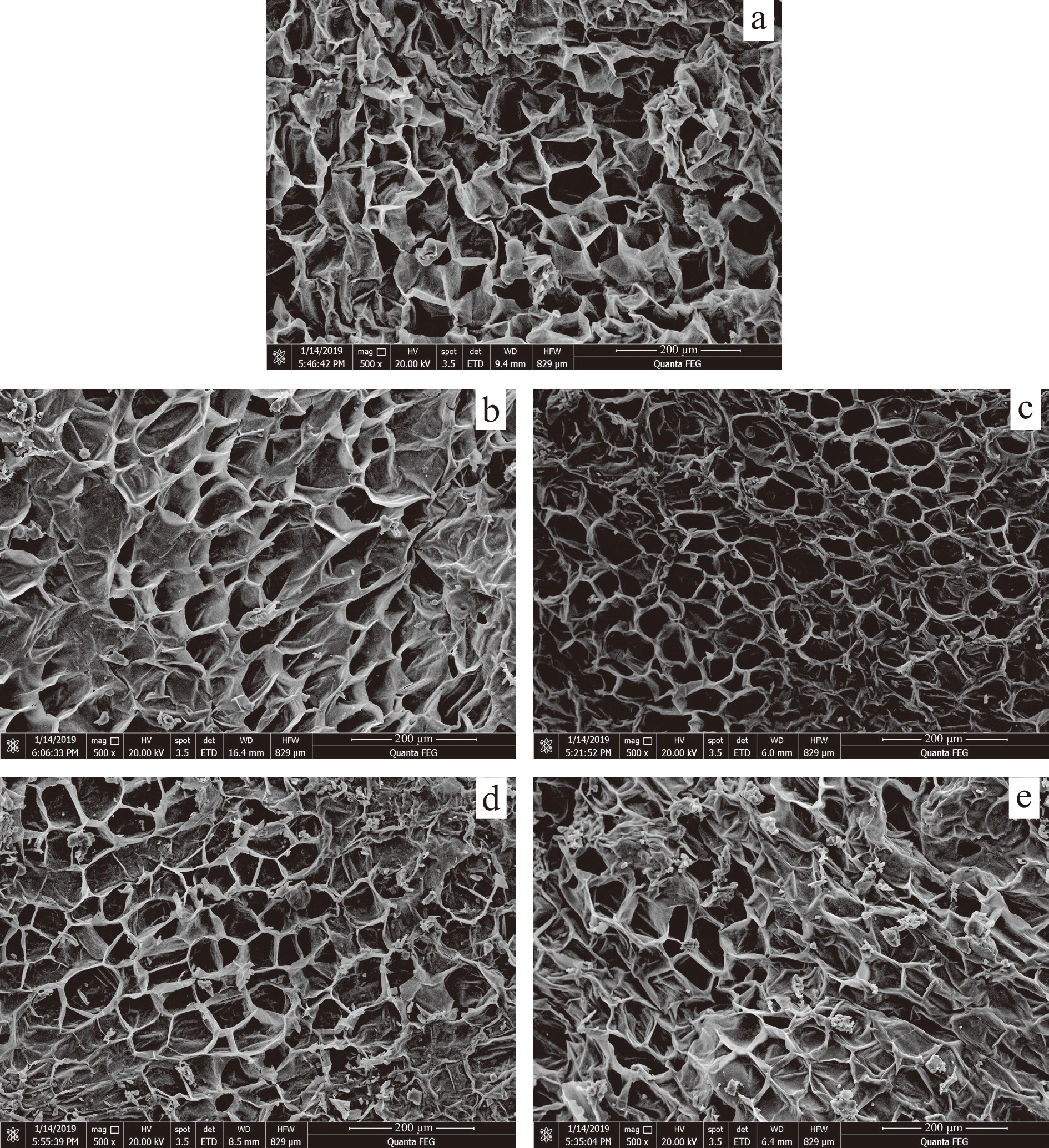
表 3 新鲜及微波真空干燥菊芋片的色泽参数

Table 3. Color parameters of fresh and microwave vacuum dried Jerusalem artichoke slices

	新鲜样品	MVD-1.28	MVD-1.69	MVD-2.32	MVD-2.70	MVD-3.04
L^*	62.97±2.77^c	63.70±0.62^c	64.89±0.20^b	69.05±0.41^a	68.97±0.34^a	68.16±0.18^a
a^*	1.75±0.62^e	5.89±0.27^a	4.77±0.27^b	4.35±0.06^c	4.25±0.08^c	3.71±0.14^d
b^*	11.59±1.83^e	21.37±0.47^a	18.79±0.30^b	18.34±0.42^b	18.18±0.25^b	17.02±0.18^c
∆E		10.67±0.49^a	8.04±0.27^c	9.46±1.37^b	9.26±0.19^b	7.76±0.12^d
注：同行数据不同字母表示数据之间存在显著性差异（P<0.05）。

下载: 导出CSV

| 显示表格

图 5 微波真空干燥菊芋片照片

Figure 5. Photos of microwave vacuum dried Jerusalem artichoke slices

下载: 全尺寸图片幻灯片

从图6中可知，干燥菊芋均呈现蜂窝状结构，且截面部分区域存在孔洞。1.28 W/g的干燥样品细胞轮廓清晰可见，但细胞皱缩明显（图6a），因为低微波强度下，物料干燥速率相对较慢，不具有显著的膨化效果，且干燥期间物料水分流失会使细胞失去膨胀压而收缩。随微波强度的增大，样品的细胞结构更加规则、整齐，且出现明显的孔洞，这是由于微波加热使物料水分由内向外扩散的过程中保持较小的表面张力，且真空度及一定的微波强度能提高水分的汽化强度，抑制了物料细胞及孔隙的收缩，故呈现较好的组织结构。在高微波强度下，样品部分组织结构坍塌、细胞内物质释放并发生凝结，导致细胞大小不一，在3.04 W/g下干燥的样品尤为明显，如如图6e所示，这是因为微波加热导致物料内外同时升温，当物料内水分汽化速率过快时，水蒸气产生的应力会超过物料组织结构的承受力，致使细胞破裂，内容物外泄。

图 6 微波真空干燥菊芋片的电子显微镜图（500×）

Figure 6. SEM figures for microwave vacuum dried Jerusalem artichoke slices

注：a：1.28 W/g；b：1.69 W/g；c：2.32 W/g；d：2.70 W/g； e： 3.04 W/g。

下载: 全尺寸图片幻灯片

3. 结论

菊芋微波真空干燥特性与微波强度有关，强度越大，干燥时间越短。除1.28 W/g外，其他强度的干燥过程均存在升速、恒速和降速3个阶段。采用Weibull分布函数对干燥曲线进行拟合，决定系数（R²）在0.996～0.998之间，尺度参数（α）随微波强度增加而减小，形状参数β介于1.314～2.175之间，说明干燥并非完全由内部扩散控制。基于Dincer模型的拟合结果，滞后因子（G）介于1.043～1.188，表明干燥前期存在升速阶段；毕渥数（Bi）为0.179～5.762，说明干燥过程菊芋温度变化由内部导热和边界对流换热共同控制。估算水分扩散系数D_cal在5.922×10⁻⁸～2.717×10⁻⁷ m²/s之间，而有效水分扩散系数D_eff在7.570×10⁻⁷～1.799×10⁻⁵ m²/s之间，且均随着微波强度的升高而增大。依据Arrhenius方程得到的菊芋微波真空干燥的活化能E_a为2.306 kJ/（mol·K）。

微波真空干燥导致菊芋产生明显色差，ΔE值均大于3，且微波强度愈大，样品a^*和b^*值越小；2.32 W/g 干燥菊芋的L^*值最大，为69.05。SEM结果显示，适宜微波强度下（1.69和2.32 W/g），样品细胞结构规则、整齐，且存在明显的孔洞，但在低微波强度下样品细胞结构皱缩严重，相反在高强度下微波加热则会导致部分组织结构塌陷，细胞内物质外泄发生凝结。本研究为菊芋的微波真空干燥模拟提供理论支撑，同时为其他干燥条件选择和干燥设备设计提供依据。

图 1 微波真空干燥设备示意图

Figure 1. Schematic diagram of microwave vacuum drying equipment

下载: 全尺寸图片幻灯片

图 2 不同微波强度下菊芋片的干燥曲线

Figure 2. Drying curves of jerusalem artichoke slices under different levels of microwave intensity

下载: 全尺寸图片幻灯片

图 3 不同微波强度下菊芋片的干燥速率曲线

Figure 3. Curves of drying rates of Jerusalem artichoke slices at different levels of microwave intensity

下载: 全尺寸图片幻灯片

图 4 不同微波强度下Weibull分布函数（a）和Dincer模型（b）的预测值与试验值比较

Figure 4. Comparison of the predicted values by the Weibull (a) and Dincer (b) model and experimental values of moisture ratio at varying time under different microwave intensities

下载: 全尺寸图片幻灯片

图 5 微波真空干燥菊芋片照片

Figure 5. Photos of microwave vacuum dried Jerusalem artichoke slices

下载: 全尺寸图片幻灯片

图 6 微波真空干燥菊芋片的电子显微镜图（500×）

Figure 6. SEM figures for microwave vacuum dried Jerusalem artichoke slices

注：a：1.28 W/g；b：1.69 W/g；c：2.32 W/g；d：2.70 W/g； e： 3.04 W/g。

下载: 全尺寸图片幻灯片

表 1 基于Weibull分布函数和Dincer模型的菊芋干燥曲线拟合结果

Table 1 Simulation results of drying curves of Jerusalem artichoke slices based on Weibull and Dincer model

微波强度（W/g）	Weibull 分布模型				Dincer模型
微波强度（W/g）	尺度参数α （min）	形状参数β	R²	RMSE	滞后因子G	干燥系数S （s^-1）	R²	RMSE
1.28	16.983±0.16^a	2.175±0.06^a	0.996	0.0213	1.188±0.07^a	0.071±0.006^a	0.910	0.105
1.69	11.581±0.11^b	1.598±0.03^b	0.998	0.0150	1.131±0.04^ab	0.101±0.006^b	0.966	0.0601
2.32	6.563±0.11^c	1.314±0.04^c	0.996	0.0180	1.069±0.03^bc	0.168±0.007^c	0.986	0.0345
2.70	5.958±0.08d	1.330±0.03^c	0.998	0.0134	1.067±0.03^bc	0.185±0.010^c	0.985	0.0378
3.04	3.701±0.07^e	1.341±0.05^c	0.998	0.0150	1.043±0.03^c	0.293±0.018^d	0.985	0.0373
注：同列数据不同字母表示数据间存在显著性差异（P<0.05）；表2同。

下载: 导出CSV

表 2 Weibull分布函数和Dincer模型参数的计算结果

Table 2 Results of Weibull and Dincer model parameters

微波强度（W/g）	D^*_eff （×10⁻⁹， m²/s）	D_cal （×10⁻⁸， m²/s）	D_eff （×10⁻⁷， m²/s）	毕渥数 Bi	特征根 μ	传质系数k （×10⁻³，m/s）
1.28	2.353±0.16^e	5.922±0.05^e	0.7570±0.04^a	5.762±0.29^a	1.225 ±0.06^a	2.181±0.11^a
1.69	2.872±0.10^d	8.684±0.08^d	1.646±0.08^b	1.543±0.08^b	0.991±0.05^b	1.270±0.06^c
2.32	4.138±0.09^c	15.326±0.25^c	5.954±0.30^c	0.348±0.02^c	0.672±0.03^c	1.035±0.05^d
2.70	4.982±0.14^b	16.881±0.22^b	6.844±0.34^d	0.328±0.02^c	0.658±0.03^c	1.122±0.06^d
3.04	7.546±0.32^a	27.178±0.51^a	17.985±0.90^e	0.179±0.009^c	0.511±0.03^d	1.610±0.08^b
注：“D^*_eff”表示依据Fick第二定律的计算得到的水分扩散系数；“D_cal”表示基于Weibull分布函数的计算结果；“D_eff”表示基于Dincer模型的计算结果。

下载: 导出CSV

表 3 新鲜及微波真空干燥菊芋片的色泽参数

Table 3 Color parameters of fresh and microwave vacuum dried Jerusalem artichoke slices

	新鲜样品	MVD-1.28	MVD-1.69	MVD-2.32	MVD-2.70	MVD-3.04
L^*	62.97±2.77^c	63.70±0.62^c	64.89±0.20^b	69.05±0.41^a	68.97±0.34^a	68.16±0.18^a
a^*	1.75±0.62^e	5.89±0.27^a	4.77±0.27^b	4.35±0.06^c	4.25±0.08^c	3.71±0.14^d
b^*	11.59±1.83^e	21.37±0.47^a	18.79±0.30^b	18.34±0.42^b	18.18±0.25^b	17.02±0.18^c
∆E		10.67±0.49^a	8.04±0.27^c	9.46±1.37^b	9.26±0.19^b	7.76±0.12^d
注：同行数据不同字母表示数据之间存在显著性差异（P<0.05）。

下载: 导出CSV

参考文献(31)

[1]	KHUENPET K, JITTANIT W, SIRISANSANEEYAKUL S, et al. Inulin powder production from Jerusalem artichoke (Helianthus tuberosus L.) tuber powder and its application to commercial food products[J]. Journal of Food Processing and Preservation,2017,41(4):e13097. doi: 10.1111/jfpp.13097
[2]	CHENG X F, ADHIKARI B, XIE A G, et al. Moisture sorption behaviour and thermodynamic properties of adsorbed water of Jerusalem artichoke (Helianthus tuberosus L.) powder[J]. International Food Research Journal,2020,27(3):505−515.
[3]	RADOVANOVIC A, STOJCESKA V, PLUNKETT A, et al. The use of dry Jerusalem artichoke as a functional nutrient in developing extruded food with low glycaemic index[J]. Food Chemistry,2015,177:81−88. doi: 10.1016/j.foodchem.2014.12.096
[4]	TAMAS A, MOHAMED T, TAREK-TILISTYAK J, et al. Comparative effects of three different drying methods on drying kinetics and quality of Jerusalem artichoke (Helianthus tuberosus L.)[J]. Journal of Food Processing and Preservation,2017,43(3):e12971.
[5]	DOYMAZ I. Effect of pre-treatment and air temperature on drying kinetics and quality of Jerusalem artichoke[J]. Studii şi Cercetări Stiinţifice CICBIA,2018,19(4):395−409.
[6]	曾目成, 毕金峰, 陈芹芹, 等. 基于Weibull分布函数猕猴桃切片微波真空干燥过程模拟及应用[J]. 中国食品学报,2015,15(6):129−135. [ZENG M C, BI J F, CHEN Q Q, et al. Weibull distribution for modeling microwave vacuum drying of kiwifruit slices and its application[J]. Journal of Chinese Institute of Food Science and Technology,2015,15(6):129−135.
[7]	DONG W, CHENG K, HU R, et al. Effect of microwave vacuum drying on the drying characteristics, color, microstructure, and antioxidant activity of green coffee beans[J]. Molecules,2018,23(5):1146−1161. doi: 10.3390/molecules23051146
[8]	JIANG N, LIU C Q, LI D, et al. Effect of thermosonic pretreatment on drying kinetics and energy consumption of microwave vacuum dried Agaricus bisporus slices[J]. Journal of Food Engineering,2016,177:21−30. doi: 10.1016/j.jfoodeng.2015.12.012
[9]	BAI-NGEW S, THERDTHAI N, DHAMVITHEE P. Characterization of microwave vacuum-dried durian chips[J]. Journal of Food Engineering,2011,104:114−122. doi: 10.1016/j.jfoodeng.2010.12.003
[10]	代建武, 杨升霖, 王杰, 等. 微波真空干燥对香蕉片干燥特性及品质的影响[J]. 农业机械学报,2020,51(S1):493−500. [DAI J W, YANG S L, WANG J, et al. Effect of microwave vacuum drying conditions on drying characteristics and texture sructure of banana chips[J]. Transactions of the Chinese Society for Agricultural Machinery,2020,51(S1):493−500. doi: 10.6041/j.issn.1000-1298.2020.S1.058
[11]	LAGNIKA C, JIANG N, SONG J, et al. Effects of pretreatments on properties of microwave-vacuum drying of sweet potato slices[J]. Drying Technology,2019,37(15):1901−1914. doi: 10.1080/07373937.2018.1543702
[12]	薛广, 李敏, 关志强. 基于Weibull函数的超声渗透罗非鱼片真空微波干燥模拟[J]. 食品与发酵工业,2020,46(1):157−165. [XUE G, LI M, GUAN Z Q. Simulation of vacuum microwave drying of tilapia fillets by ultrasonic penetration based on Weibull function[J]. Food and Fermentation Industries,2020,46(1):157−165.
[13]	TAYYAB RASHID M, AHMED JATOI M, SAFDAR B, et al. Modeling the drying of ultrasound and glucose pretreated sweet potatoes: The impact on phytochemical and functional groups[J]. Ultrasonics Sonochemistry,2020,68:105226. doi: 10.1016/j.ultsonch.2020.105226
[14]	ZHAO Y T, WANG W W, ZHENG B D, et al. Mathematical modeling and influence of ultrasonic pretreatment on microwave vacuum drying kinetics of lotus (Nelumbo nucifera Gaertn.) seeds[J]. Drying Technology,2016,35(5):553−563.
[15]	张卫鹏, 肖红伟, 高振江, 等. 中短波红外联合气体射流干燥提高茯苓品质[J]. 农业工程学报,2015,31(10):269−276. [ZHANG W P, XIAO H W, GAO Z J, et al. Improving quality of Poria cocos using infrared radiation combined with air impingement drying[J]. Transactions of the Chinese Society of Agricultural Engineering,2015,31(10):269−276. doi: 10.11975/j.issn.1002-6819.2015.10.036
[16]	巨浩羽, 赵海燕, 张菊, 等. 基于Dincer模型不同干燥方式下光皮木瓜干燥特性研究[J]. 中草药,2020,51(15):3911−3921. [JU H Y, ZHAO H Y, ZHANG J, et al. Drying characteristics of Chaenomeles sinensis with different drying methods based on Dincer model[J]. Chinese Traditional and Herbal Drugs,2020,51(15):3911−3921. doi: 10.7501/j.issn.0253-2670.2020.15.010
[17]	XIE L, ZHENG Z A, MUJUNNDAR A S, et al. Pulsed vacuum drying (PVD) of wolfberry: Drying kinetics and quality attributes[J]. Drying Technology,2018,36(12):1501−1514. doi: 10.1080/07373937.2017.1414055
[18]	KARACABEY E, BUZRUL S. Modeling and predicting the drying kinetics of apple and pear: Application of the Weibull model[J]. Chemical Engineering Communications,2017,204(5):573−579. doi: 10.1080/00986445.2017.1291427
[19]	JU H Y, ZHAO S H, MUJUNNDAR A S, et al. Energy efficient improvements in hot air drying by controlling relative humidity based on Weibull and Bi-Di models[J]. Food and Bioproducts Processing,2018,111:20−29. doi: 10.1016/j.fbp.2018.06.002
[20]	XIE Y, GAO Z, LIU Y, et al. Pulsed vacuum drying of rhizoma dioscoreae slices[J]. LWT-Food Science and Technology,2017,80:237−249. doi: 10.1016/j.lwt.2017.02.016
[21]	MCMINN W A M. Prediction of moisture transfer parameters for microwave drying of lactose powder using Bi-G drying correlation[J]. Food Research International,2004,37(10):1041−1047. doi: 10.1016/j.foodres.2004.06.013
[22]	王红提, 郭康权, 李鹏, 等. 疏解棉秆的微波干燥动力学及能耗分析[J]. 农业工程学报,2015,31(19):294−301. [WANG H T, GUO K Q, LI P, et al. Microwave drying kinetics and energy consumption analysis of extruded cotton stalks[J]. Transactions of the Chinese Society of Agricultural Engineering,2015,31(19):294−301. doi: 10.11975/j.issn.1002-6819.2015.19.040
[23]	WANG J, LAW C L, NEMA P K, et al. Pulsed vacuum drying enhances drying kinetics and quality of lemon slices[J]. Journal of Food Engineering,2018,224:129−138. doi: 10.1016/j.jfoodeng.2018.01.002
[24]	ARAL S, BESE A V. Convective drying of hawthorn fruit (Crataegus spp.): Effect of experimental parameters on drying kinetics, color, shrinkage, and rehydration capacity[J]. Food Chemistry,2016,210:577−584. doi: 10.1016/j.foodchem.2016.04.128
[25]	张付杰, 辛立东, 代建武, 等. 猕猴桃片旋转托盘式微波真空干燥特性分析[J]. 农业机械学报,2020,51(S1):501−508. [ZHANG F J, XIN L D, DAI J W, et al. Rotating tray microwave vacuum drying characteristics of kiwifruit slices[J]. Transactions of the Chinese Society for Agricultural Machinery,2020,51(S1):501−508. doi: 10.6041/j.issn.1000-1298.2020.S1.059
[26]	刘春泉, 严启梅, 江宁, 等. 杏鲍菇真空微波干燥特性及动力学模型[J]. 核农学报,2012,26(3):494−0498. [LIU C Q, YAN Q M, JIANG N. Properties and dynamics model of vacuum microwave dried Pleurotus eryngii[J]. Journal of Nuclear Agricultural Sciences,2012,26(3):494−0498.
[27]	孙悦, 刘云宏, 于慧春, 等. 基于Weibull分布函数的超声强化热风干燥紫薯的干燥特性及过程模拟[J]. 食品科学,2017,38(7):129−135. [SUN Y, LIU Y H, YU H C, et al. Drying characteristics and process simulation of ultrasound-assisted hot air drying of purple-fleshed sweet potato based on Weibull distribution model[J]. Food Science,2017,38(7):129−135. doi: 10.7506/spkx1002-6630-201707021
[28]	江宁. 低频热超声对双孢菇微波真空干燥效能及热电物理特性的影响[D]. 南京: 南京农业大学, 2018. JIANG N. Effect of low frequency thermosonication on efficiency and thermoelectric physical characteristics of Agaricus bisporus under microwave vacuum drying[D]. Nanjing: Nanjing Agricultural University, 2018.
[29]	潘小莉, 张帆, 刘永富, 等. 基于Weibull分布函数的龙眼果肉微波真空干燥模拟研究[J]. 农机化研究,2021(4):179−184. [PAN X L, ZHANG F, LIU Y F, et al. Research and modeling microwave vacuum drying of peeled longan based on Weibull distribution function[J]. Journal of Agricultural Mechanization Research,2021(4):179−184. doi: 10.3969/j.issn.1003-188X.2021.04.033
[30]	XIAO H W, BAI J W, XIE L, et al. Thin-layer air impingement drying enhances drying rate of American ginseng (Panax quinquefolium L.) slices with quality attributes considered[J]. Food and Bioproducts Processing,2015,94:581−591. doi: 10.1016/j.fbp.2014.08.008
[31]	ZHAO Y, JIANG Y, ZHENG B, et al. Influence of microwave vacuum drying on glass transition temperature, gelatinization temperature, physical and chemical qualities of lotus seeds[J]. Food Chemistry,2017,228:167−176. doi: 10.1016/j.foodchem.2017.01.141

施引文献(16)

期刊类型引用(13)

1.	巨浩羽，张卫鹏，于贤龙，王庆惠，高振江，肖红伟. 恒温下相对湿度对果蔬热风干燥特性和品质的影响及调控. 农业工程学报. 2024(02): 29-40 . 百度学术
2.	陈静，方晓纯，林波，吴妃妃，郑凤锦，陈赶林. 多维度解析干燥方式对荔浦芋品质特性的影响. 南方农业学报. 2024(01): 199-206 . 百度学术
3.	胡轶娟，浦锦宝，徐攀，童晔玲，楼柯浪，梁卫青. 前胡切片微波真空干燥特性分析及模拟. 中国现代应用药学. 2024(10): 1343-1349 . 百度学术
4.	袁迪，李洋，陈丰，张欣硕，黄积微. 蓝莓微波冷冻干燥特性及品质分析. 中国食品学报. 2024(06): 248-263 . 百度学术
5.	马玉荷，田晓菊，王应强，赵红霞，宋嘉玲. 热风温度对苹果丁微波对流耦合加热干燥特性与品质的影响. 食品与发酵工业. 2024(16): 77-84 . 百度学术
6.	李静慧，浦锦宝，梁卫青，徐攀，童晔玲，楼柯浪，胡轶娟. 前胡切片微波真空干燥过程颜色变化分析及混合建模. 浙江中医杂志. 2024(12): 1114-1116 . 百度学术
7.	李瑞丽，尹冬辰，王新惠，许利平，张峻松，高阳. 干燥方式对红枣片动力学及挥发性成分的影响. 精细化工. 2023(02): 297-304 . 百度学术
8.	林雅文，刘佳晨，牛慧玲，谢永康，励建荣，李学鹏. 南美白对虾中短波红外干燥特性及模型拟合. 食品安全质量检测学报. 2023(09): 137-145 . 百度学术
9.	马凯迪，李莹，柴智，马恺扬，宋欣欣. 即食海苔风味酥脆虾仁的加工工艺及品质分析. 食品研究与开发. 2023(12): 89-96 . 百度学术
10.	张倩，李世榆，李秀辰，母刚，戴逸俊，张国琛. 裙带菜微波真空干燥质热传递特性与品质优化. 食品与机械. 2022(07): 166-173 . 百度学术
11.	叶鹏飞，耿政，王珂，傅虹飞，陈香维，刘惠敏，王云阳. 腐殖酸肥料射频真空干燥特性. 农业工程学报. 2022(09): 306-314 . 百度学术
12.	李盼盼，胡钦锴，张敏. 微波真空干燥技术研究进展. 食品安全导刊. 2022(20): 175-177 . 百度学术
13.	巨浩羽，张卫鹏，张鹏飞，张琦，高振江，肖红伟. 基于毕渥数的果蔬阶段降湿热风干燥特性. 农业工程学报. 2022(12): 317-324 . 百度学术

其他类型引用(3)

资源附件(0)

图(6) / 表(3)

计量

文章访问数: 214
HTML全文浏览量: 72
PDF下载量: 16
被引次数: 16

1. 材料与方法
1.1 材料与仪器
1.2 样品制备与处理
1.3 干燥曲线拟合及参数计算方法
1.3.1 干燥参数计算
1.3.2 Weibull分布函数
1.3.3 Dincer模型
1.3.4 水分有效扩散系数（D*eff）计算
1.3.5 活化能计算
1.4 色泽测定
1.5 微观结构观察
1.6 数据处理
2. 结果与分析
2.1 菊芋微波真空干燥特性
2.2 微波真空干燥曲线拟合结果分析
2.3 有效水分扩散系数及活化能的确定
2.4 色泽和微观结构分析
3. 结论

1. 材料与方法
1.1 材料与仪器
1.2 样品制备与处理
1.3 干燥曲线拟合及参数计算方法
1.3.1 干燥参数计算
1.3.2 Weibull分布函数
1.3.3 Dincer模型
1.3.4 水分有效扩散系数（D^*_eff）计算
1.3.5 活化能计算
1.4 色泽测定
1.5 微观结构观察
1.6 数据处理
2. 结果与分析
2.1 菊芋微波真空干燥特性
2.2 微波真空干燥曲线拟合结果分析
2.3 有效水分扩散系数及活化能的确定
2.4 色泽和微观结构分析
3. 结论

参考文献(31)

施引文献

资源附件(0)

菊芋微波真空干燥过程的水分扩散特性及模型拟合

作者简介: 程新峰（1981−），男，博士，副教授，研究方向：农业资源综合利用与开发，E-mail：chxf0110194@163.com

通讯作者: 李宁（1989−），女，硕士，讲师，研究方向：果蔬精深加工及副产品综合利用，E-mail：shning1989@ahnu.edu.cn

计量

出版历程